
Zadanie Akcja komandosów (akc)
Pomóż nam usprawnić bazę zadań!
Akcja komandosów
Limit pamięci: 32 MB
Na Pustyni Błędowskiej odbywa się w tym roku Bardzo Interesująca i Widowiskowa Akcja Komandosów (BIWAK). Podstawowym elementem BIWAK-u ma być neutralizacja bomby, która znajduje się gdzieś na pustyni, jednak nie wiadomo dokładnie gdzie.
Pierwsza część akcji to desant z powietrza. Z helikoptera krążącego nad pustynią, wyskakują pojedynczo, w ustalonej kolejności komandosi. Gdy któryś z komandosów wyląduje w jakimś miejscu, okopuje się i już się z nie rusza z miejsca. Dopiero potem może wyskoczyć kolejny komandos.
Dla każdego komandosa określona jest pewna odległość rażenia. Jeśli komandos przebywa w tej odległości (lub mniejszej) od bomby, to w przypadku jej ewentualnej eksplozji zginie. Dowództwo chce zminimalizować liczbę komandosów biorących udział w akcji, ale chce mieć pewność, że w przypadku wybuchu bomby, przynajmniej jeden z komandosów przeżyje.
Na potrzeby zadania przyjmujemy, że Pustynia Błędowska jest
płaszczyzną, a komandosów, którzy się okopali utożsamiamy z punktami.
Mamy dany ciąg kolejno mogących wyskoczyć komandosów.
Żaden z nich nie może opuścić swojej kolejki, tzn. jeśli 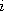 -ty
komandos wyskakuje z samolotu, to wszyscy poprzedni wyskoczyli
już wcześniej.
Dla każdego z komandosów znamy jego odległość rażenia oraz
współrzędne punktu, w którym wyląduje, o ile w ogóle wyskoczy.
-ty
komandos wyskakuje z samolotu, to wszyscy poprzedni wyskoczyli
już wcześniej.
Dla każdego z komandosów znamy jego odległość rażenia oraz
współrzędne punktu, w którym wyląduje, o ile w ogóle wyskoczy.
Zadanie
Napisz program, który:
- wczyta ze standardowego wejścia opisy komandosów,
- wyznaczy minimalną ilość komandosów, którzy muszą wyskoczyć,
- wypisze wynik na standardowe wyjście.
Wejście
W pierwszym wierszu standardowego wejścia zapisana jest jedna
liczba całkowita  (
( ) - liczba komandosów.
W kolejnych
) - liczba komandosów.
W kolejnych  wierszach opisani są komandosi - po jednym w wierszu.
Opis każdego komandosa składa się z trzech liczb całkowitych:
wierszach opisani są komandosi - po jednym w wierszu.
Opis każdego komandosa składa się z trzech liczb całkowitych:
 ,
, 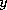 i
i  (
( ,
,  .
Punkt
.
Punkt  to miejsce, gdzie wyląduje komandos, a
to miejsce, gdzie wyląduje komandos, a  to jego
odległość rażenia.
Jeśli komandos znajdzie się w odległości
to jego
odległość rażenia.
Jeśli komandos znajdzie się w odległości  lub mniejszej od bomby,
to w przypadku jej wybuchu zginie.
lub mniejszej od bomby,
to w przypadku jej wybuchu zginie.
Wyjście
W pierwszym i jedynym wierszu standardowego wyjścia Twój program powinien zapisać jedną liczbę całkowitą - minimalną liczbę komandosów, którzy muszą wyskoczyć, aby zapewnić, że co najmniej jeden z nich przeżyje, lub jedno słowo NIE jeśli nie jest możliwe, aby mieć pewność, że któryś z komandosów przeżyje.
Przykład
Dla danych wejściowych:
5 2 2 4 7 2 3 4 3 1 5 7 1 8 7 1
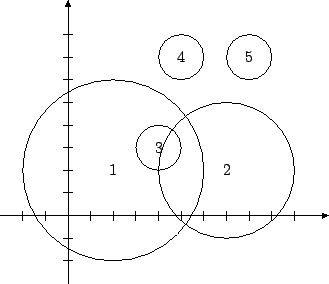
poprawną odpowiedzią jest:
4
Uwaga
To zadanie można rozwiązać używając typów zmiennopozycyjnych:
- w Pascalu: double lub extended,
- w C oraz C++: double lub long double.
Autor zadania: Szymon Acedański.
Kontakt
In the event of technical difficulties with Szkopuł, please contact us via email at [email protected].
If you would like to talk about tasks, solutions or technical problems, please visit our Discord servers. They are moderated by the community, but members of the support team are also active there.

 English
English